| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 소형기관차
- 2869
- node.js
- JSP
- SOCKET
- HTTP
- 달팽이는올라가고싶다
- SWEA
- 17822
- GitHub
- web
- react
- boj
- 비동기
- 17471
- Java
- npm
- 1868
- 카카오코드페스티벌
- Git
- JavaScript
- 백준
- staged
- 타겟넘버
- commited
- 파핑파핑지뢰찾기
- 응답코드
- graph
- Ajax
- 알고리즘
- Today
- Total
devlog
[BOJ] 백준 2156 포도주시식-java 본문
문제
효주는 포도주 시식회에 갔다. 그 곳에 갔더니, 테이블 위에 다양한 포도주가 들어있는 포도주 잔이 일렬로 놓여 있었다. 효주는 포도주 시식을 하려고 하는데, 여기에는 다음과 같은 두 가지 규칙이 있다.
- 포도주 잔을 선택하면 그 잔에 들어있는 포도주는 모두 마셔야 하고, 마신 후에는 원래 위치에 다시 놓아야 한다.
- 연속으로 놓여 있는 3잔을 모두 마실 수는 없다.
효주는 될 수 있는 대로 많은 양의 포도주를 맛보기 위해서 어떤 포도주 잔을 선택해야 할지 고민하고 있다. 1부터 n까지의 번호가 붙어 있는 n개의 포도주 잔이 순서대로 테이블 위에 놓여 있고, 각 포도주 잔에 들어있는 포도주의 양이 주어졌을 때, 효주를 도와 가장 많은 양의 포도주를 마실 수 있도록 하는 프로그램을 작성하시오.
예를 들어 6개의 포도주 잔이 있고, 각각의 잔에 순서대로 6, 10, 13, 9, 8, 1 만큼의 포도주가 들어 있을 때, 첫 번째, 두 번째, 네 번째, 다섯 번째 포도주 잔을 선택하면 총 포도주 양이 33으로 최대로 마실 수 있다.
입력
첫째 줄에 포도주 잔의 개수 n이 주어진다. (1≤n≤10,000) 둘째 줄부터 n+1번째 줄까지 포도주 잔에 들어있는 포도주의 양이 순서대로 주어진다. 포도주의 양은 1,000 이하의 음이 아닌 정수이다.
출력
첫째 줄에 최대로 마실 수 있는 포도주의 양을 출력한다.
문제:https://www.acmicpc.net/problem/2156
2156번: 포도주 시식
효주는 포도주 시식회에 갔다. 그 곳에 갔더니, 테이블 위에 다양한 포도주가 들어있는 포도주 잔이 일렬로 놓여 있었다. 효주는 포도주 시식을 하려고 하는데, 여기에는 다음과 같은 두 가지 규칙이 있다. 포도주 잔을 선택하면 그 잔에 들어있는 포도주는 모두 마셔야 하고, 마신 후에는 원래 위치에 다시 놓아야 한다. 연속으로 놓여 있는 3잔을 모두 마실 수는 없다. 효주는 될 수 있는 대로 많은 양의 포도주를 맛보기 위해서 어떤 포도주 잔을 선택해야 할지 고
www.acmicpc.net
풀이
이 문제는 연속하는 잔을 두개까지만 고를 수 있기 때문에 배열을 돌면서 현재 인덱스에서 어떻게 먹는 것이 제일 많은 양을 먹는지를 생각해봐야 합니다.
우선 선택하는 방법은 3가지가 있습니다.
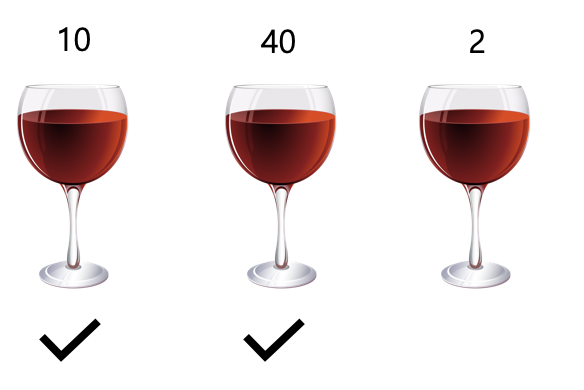
위의 그림이 첫 번째 경우입니다. (DP[i-1]이 최대인 경우)
위의 경우에서 DP[0]은 amount[0]이고 DP[1]은 amount[0] + amount[1]입니다.
그리고 DP[2]의 값을 정할 때 amount[2](=2)를 마시게 되면 세 번 연속으로 와인을 마실 수는 없기 때문에 10 혹은 40 중 하나를 마시고 2를 마셔야 하는데 그러면 최대 값이 안 나오기 때문에 2(amount[2])를 마시지 않고 10, 40을 마시는 경우를 택하는데 이것이 DP[1]과 같기 때문에 DP[2] = DP[1]이 됩니다.
이 경우 DP[i] = DP[i-1]이 됩니다.

위의 경우가 두번째 경우입니다. (DP[i-2]+amount[i]가 최대인 경우)
위의 경우에서 4번째 와인잔에서 최대값을 구할 때 10과 13을 마신다면 6,9를 못 마시기 때문에 최댓값이 나오지 않습니다.
이 경우 현재 자리에 있는 9를 마시고 두번째 전에 있는(i-2) 자리의 최댓값을 더하는 것(DP[i-2])이 최댓값이 나오게 됩니다.
그러므로 DP[i] = DP[i-2] + amount[i] 가 됩니다.

위의 경우가 세번째 방법입니다. (DP[i-3] + amount[i] + amount[i-1] 이 최대인 경우)
위의 경우에서 마지막 와인잔에 멈췄을 때는 현재 자리에 있는 와인잔(20)을 마시고 바로 전에 있는 와인잔(4)을 마시고 그다음 연속해서 2번 안 마시고 i-4번째의 최댓값을 더하는 경우입니다.
그런데 이 경우는 생각해보면 i-4까지 갈 필요가 없습니다.
DP[i-3]의 값이 위에서 봤던 첫 번째 경우이므로 DP[i-4]와 같기 때문입니다.
즉 DP[i] = amount[i] + amount[i-1] + DP[i-3]이 됩니다.
이 세 경우만 확인해주면 되므로 최대 값을 찾을 때 이 3가지 중 제일 큰 값을 DP[i]값으로 정해주면 답을 얻을 수 있습니다.
'Algorithm > BOJ' 카테고리의 다른 글
| [BOJ] 백준 2309 일곱 난쟁이-java (0) | 2019.10.05 |
|---|---|
| [BOJ] 백준 11724 연결 요소의 개수-java (0) | 2019.09.28 |
| [BOJ] 백준 5567 결혼식-java (0) | 2019.06.21 |
| [BOJ] 백준 9933 민균이의비밀번호-java (0) | 2019.04.30 |
| [BOJ] 백준 2252 줄세우기-java (0) | 2019.03.21 |


